[最も共有された！ √] f(x)=x^2 what is g(x) (3 3) apex 122592

Odd functions If f ( x) is an odd function, then for every x and − x in the domain of f, − f ( x) = f ( − x) Graphically, this means that the function is rotationally symmetric with respect to the origin Thus, rotations of 180 ∘ or any multiple of 180 ∘ do not affect the function's appearance Good examples of odd functionsNot a problem Unlock StepbyStep Extended KeyboardSolution for g (x)=3f (x2)1 equation Simplifying g (x) = 3f (x 2) 1 Multiply g * x gx = 3f (x 2) 1 Reorder the terms gx = 3f (2 x) 1 gx = (2 * 3f x * 3f) 1 gx = (6f 3fx) 1 Reorder the terms gx = 1 6f 3fx Solving gx = 1 6f 3fx Solving for variable 'g'

Example 16 Let F X X2 And G X 2x 1 Find F G Fg F G

F(x)=x^2 what is g(x) (3 3) apex

F(x)=x^2 what is g(x) (3 3) apex-Experts are waiting 24/7 to provide stepbystep solutions in as fast as 30 minutes!* · 2something 3 = 8x – 1 Hmmthere's gotta be a 4 x in the something otherwise i'll never get 8 x But if it's just 4 x in there then I'll end up with 8 x 3, not 8 x – 1

Help

F (x) = 2 x^2 3 x 5, f (x 3) 3 = g (x) WolframAlpha Rocket science?F (x)=3x^2 g (x)=x1 Now f (g (x))= 3×(g (x))^2 f (g (x))= 3× (x1)^2=3x^2–6x3 g (f (x))= fx1 g (f (x))= 3x^2–1/12/ · Theorem 541 The Fundamental Theorem of Calculus, Part 1 Let f be continuous on a, b and let F(x) = ∫x af(t)dt Then F is a differentiable function on (a, b), and F ′ (x) = f(x) Initially this seems simple, as demonstrated in the following example Example 541 Using the Fundamental Theorem of Calculus, Part 1

F (g (2)), g (x)=2x1, f (x)=x^2 \square!F (x) = 3/ (x1), g (x) = 2/x f (x) = 3/ (x1), g (x) = 2/x Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device · Stepbystep explanation (fg) (x) = (x² 2x 3) (x³ 4) = x²* (x³ 4) 2x* (x³ 4) 3 * (x³ 4) = x²*x³ x²*4 2x*x³ 2x* (4) 3*x³ 3 * 4 = x⁵ 4x² 2x⁴ 8x 3x³ 12 = x⁵

Given f (x) = 3x 2 – x 4, find the simplified form of the following expression, and evaluate at h = 0 This isn't really a functionsoperations question, but something like this often arises in the functionsoperations context This looks much worse than · Ex 13, 1 Deleted for CBSE Board 21 Exams only Ex 13, 2 Deleted for CBSE Board 21 Exams only Ex 13, 3 Important Deleted for CBSE Board 21 Exams only You are · 👍 Correct answer to the question The graph of g(x) shown below resembles the graph of f(x)=x^4x^2 but it has been changed somewhat just did it on apex answer is f(x)=x^4x^22 eeduanswerscom

Apex 3 Steelseries

F X X 2 What Is G X Brainly Com

 · Explanation f (x) = x −3 g(x) = x2 To find f (g(x)), plug in x2 wherever you see x in f (x) f (g(x)) = x2 − 3 f (g(4)) = (4)2 − 3 = 16 − 3 = 13Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor · (fg) (x) = x^2 x 2 Solution FOR THE OPERATION OF SUBTRACTION Given f(x) = X2 g(x) = x^2 4 Formula f(x) g(x) = (fg) (x) (fg) (x) = X2 – (x^2 4) (fg) (x) = X2 –x^2 4 (fg) (x) = –x^2 x 6 Solution FOR THE OPERATION OF MULTIPLICATION Given f(x) = X2 g(x) = x^2 4 (f*g) (x )= (X2)(x^2 4) (f*g) (x )= x^3 – 4x 2x^2 8

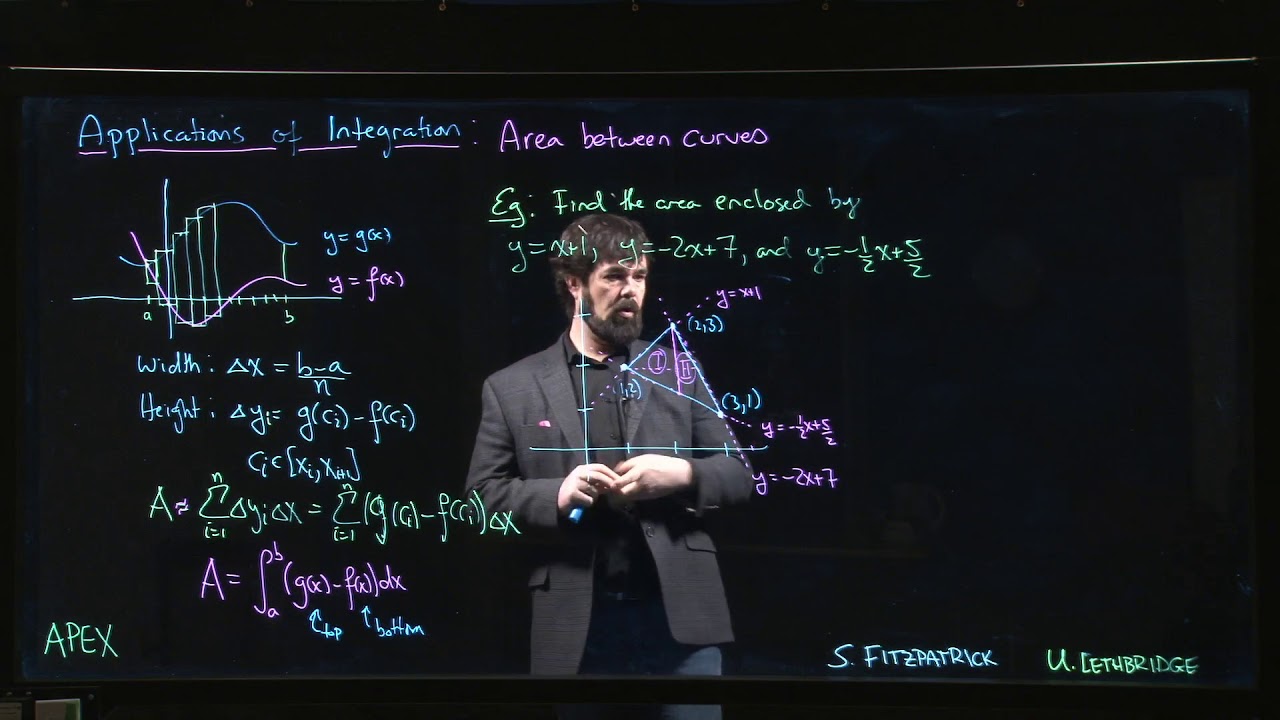
Apex Area Between Curves

The Versatility Of Ascorbate Peroxidase Aided Mapping Uncovers Insights Of The Nuclear Lamina Interactions And Function Biorxiv

 · We have g(x) = f –1 (x) ⇒ f(g(x)) = x ⇒ f'(g(x))g'(x) = 1 (i) Now, f(0) = 1 From (i), we get, f'(g(1))g'(1) = 1 Thus, g(1) = k = 0For the given functions of each composite functions f and g, find f of g, g of f, f of f, g of g · Question What is (fg)(x)?

15 3 Line Integrals Over Vector Fields Chapter 15 Vector Analysis Part Calculus Iii

If F X X And G X X Then Value Of Gof 5 4 Is Teachoo

23 Solve g3f = 0 Tiger recognizes that we have here an equation of a straight line Such an equation is usually written y=mxb ("y=mxc" in the UK) "y=mxb" is the formula of a straight line drawn on Cartesian coordinate system in which "y" is the vertical axis and "x" the horizontal axis In this formula y tells us how far up the line goesReplace the x in the f(x) equation with the value of g(x) to get (x3)cubed 2That's it When you write f(x) = x3 2 That means x can be any number, equation or function and whatever that value is, it goes into x3 2 · Answer star 48 /5 heart 18 crisforp ( f g ) ( x ) = f ( x ) g ( x ) = 2^x1 3 5x 9 = 2^x1 5x 12 ;

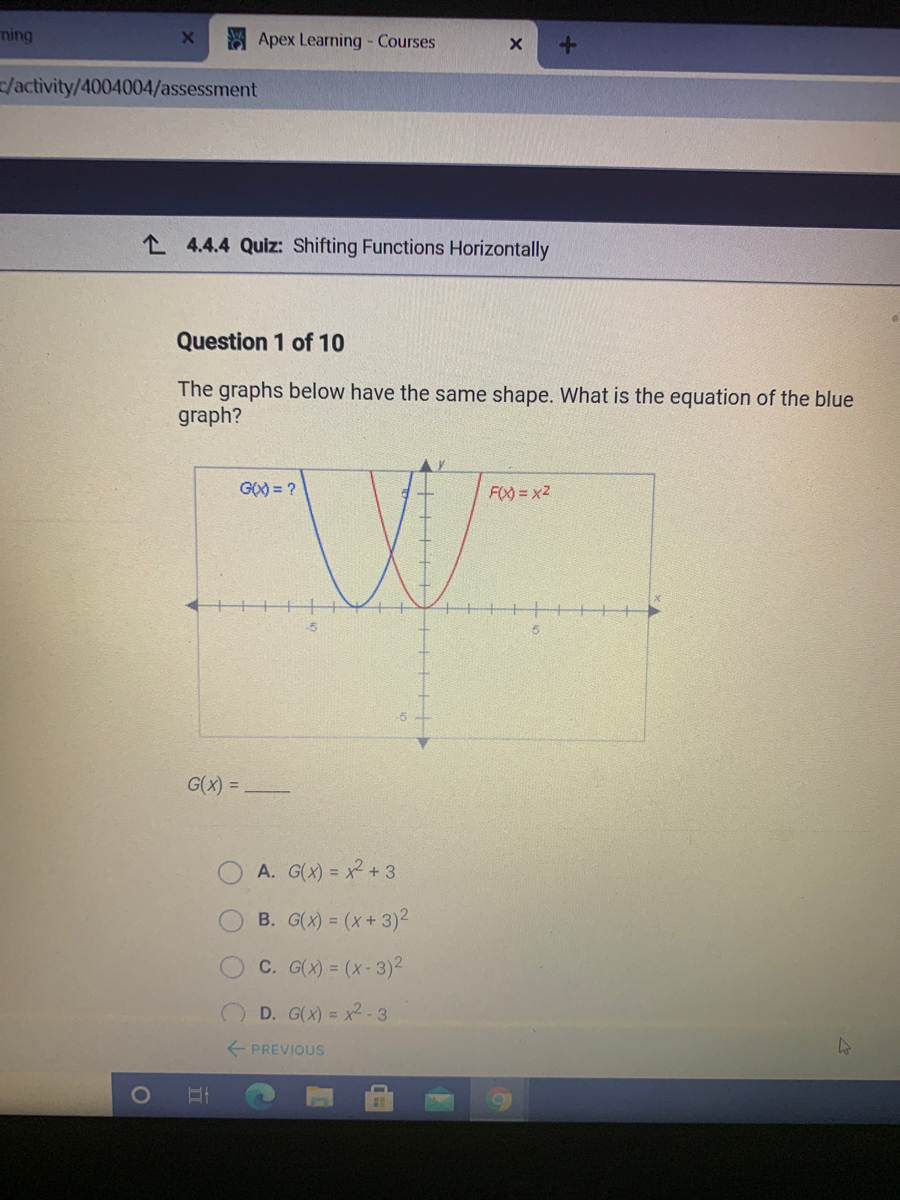
Answered A Apex Learning Courses Bartleby

F X X 2 What Is G X Brainly Com

F (x) = x 2 g (x) = 2 x f (g (x) = {g (x)} 2 ⇒ f (g (x) = {2 x} 2 = 2 2 x g (f (x)) = 2 f (x) ⇒ g (f (x)) = 2 x 2 g o f (x) = f o g (x) 2 x 2 = 2 2 x ⇒ x 2 = 2 x x 2 − 2 x = 0 x (x − 2) = 0 x = 0, 2//socraticorg/questions/howdoyoufindthedomainofgxxx1x3 Shura May 12, 15 The answer is \displaystyle {D}=\mathbb {R} {\left\lbrace {3};Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

What Are The Domain And Range Of F X 2 3 X Brainly

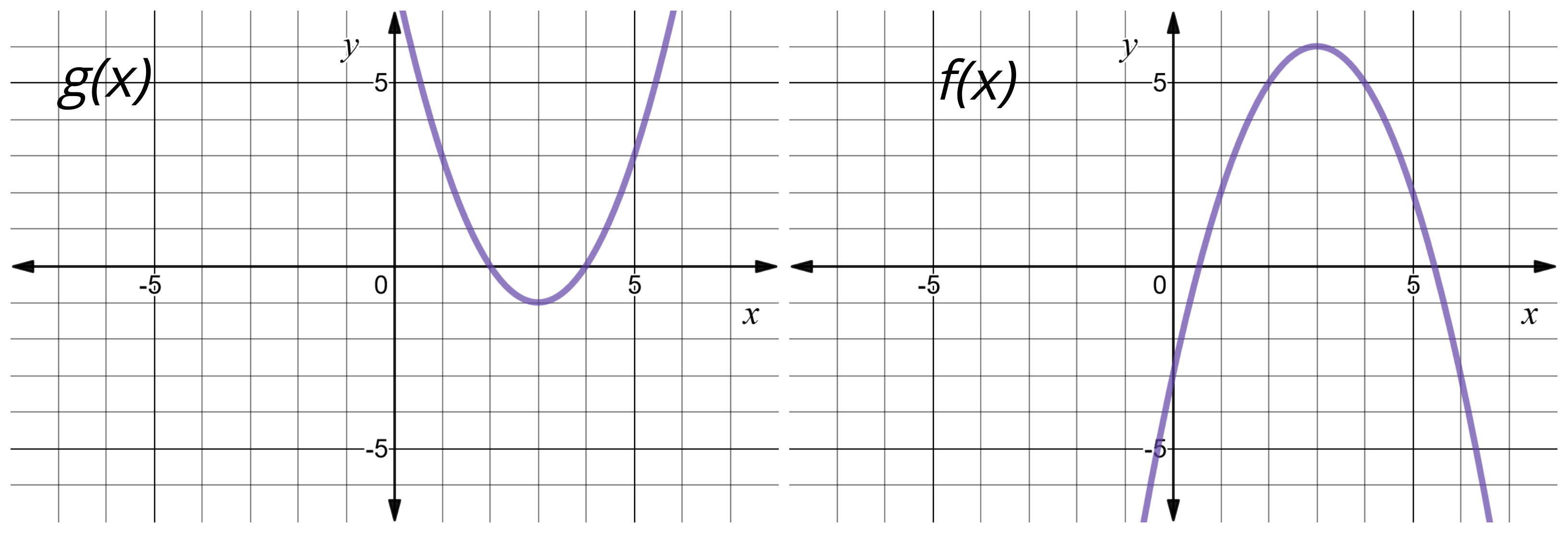
Composing Functions At A Point Expii

Find two linear functions f(x) and g(x) such that the product h(x) = f(x)g(x) is tangent to each This problem was posed by a group of teachers during a workshop in which the use of function graphers was being explored Our analysis is presented as a sort of stream of consciousness account of how one might explore the problem with the tools atThe relationships of F and G to x are defined by the equations F (x) = 3x² 1 G (x) = 2x 3 To evaluate F (G (x)), we have to replace x in F (x) by 2x 3 Doing this, we obtain F (G (x)) = 3 (2x 3)² 1 = 3 (4x² 12x 9) 1 = 12x² 36x 27 1 = 12x² 36x 28, Or = 4 (3x² · This answers this question and the next (f g)(x) means that you have to add both f(x) and g(x) (f g)(x) = x^2 − 36 x^3 2x^2 − 10

Mathematics For The Ib Diploma Analysis And Approaches Sl Draft Copy By Hodder Education Issuu

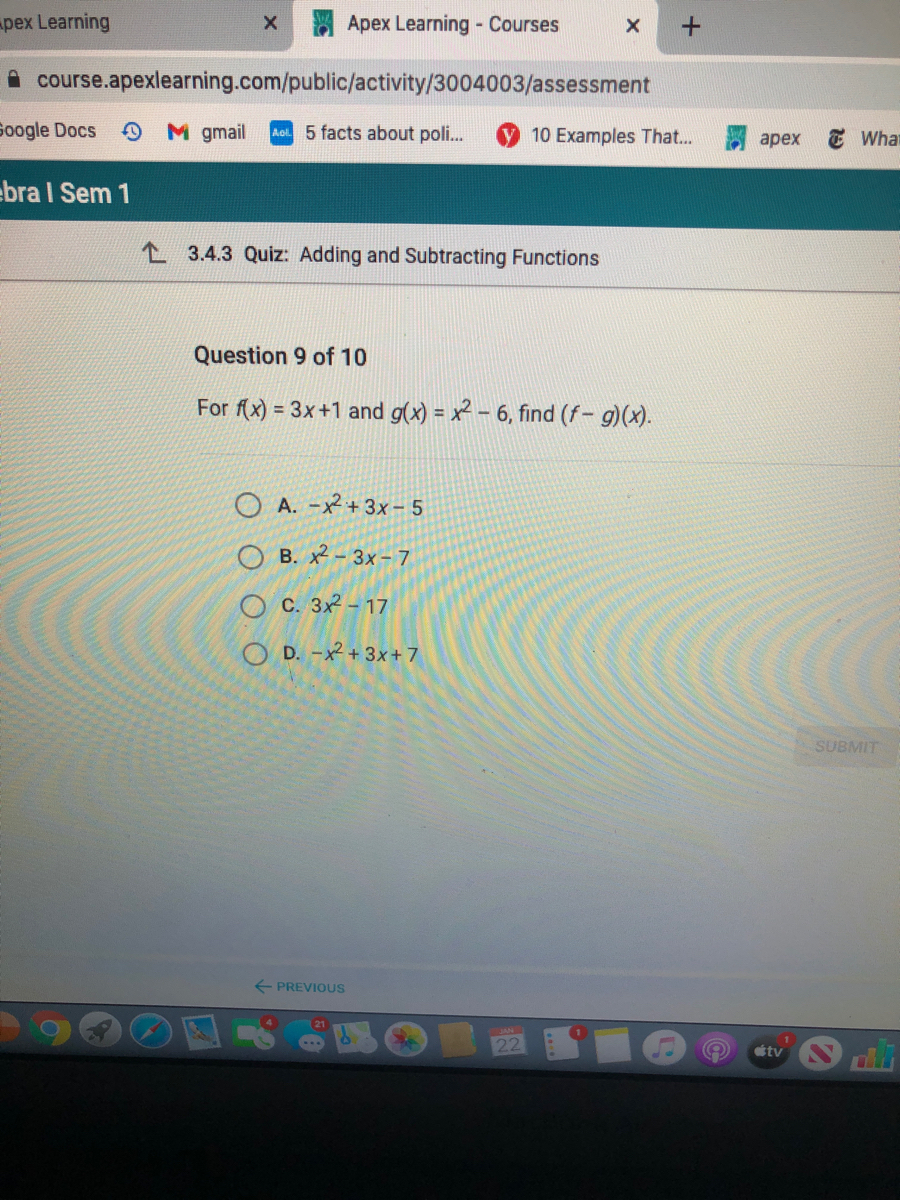
Answered Question 9 Of 10 For F X 3x 1 And Bartleby

Suppose you are given the two functions f (x) = 2x 3 and g(x) = –x 2 5Composition means that you can plug g(x) into f (x)This is written as "(f o g)(x)", which is pronounced as "fcomposeg of x"And "( f o g)(x)" means "f (g(x))"That is, you plug something in for x, then you plug that value into g, simplify, and then plug the result into f · Ex 23, 3 A function f is defined by f(x) = 2x – 5 Write down the values of (i) f(0) (ii) f(7), (iii) f(–3), Given f(x) = 2x – 5 Putting value of x in f(x) f(0) = 2 × 0 – 5 = 0 – 5 = –5 f(7) = 2 × 7 – 5 = 14 – 5 = 9 f(−3) = 2 × (−3) – 5Simple and best practice solution for g(x)=3f(x1)2 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so

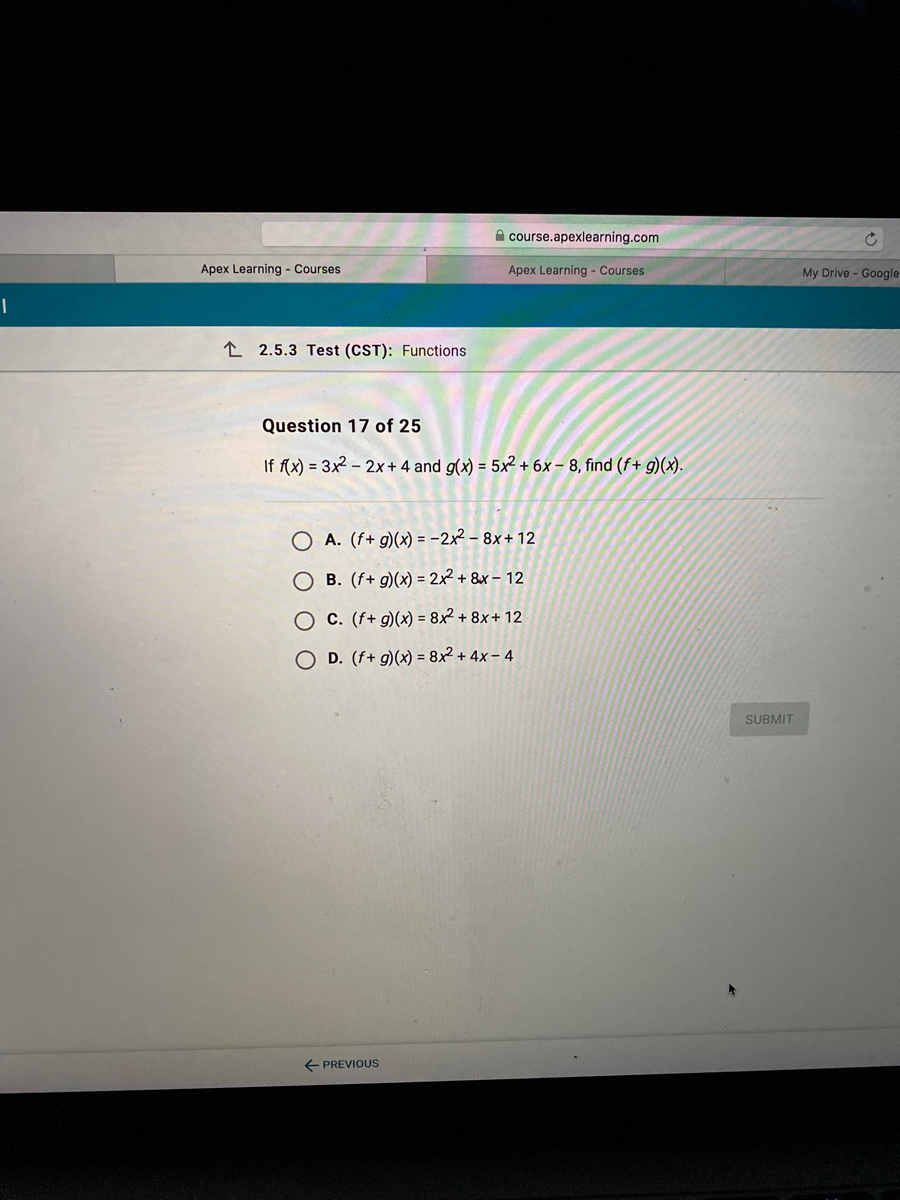
Answered If F X 3x2 2x 4 And G X 5x Bartleby

Find K So That X 2f X May Exist Where F X 2x 3 X 2 X K X 2

G(x)= x2 1 x (8) f(x) = 3x 4 (9) f( ) = 3( ) 4 (10) f(g(x)) = 3(g(x)) 4 (11) f(x2 1 x) = 3(x2 1 x) 4 (12) f(x 2 1 x) = 3x 3 x 4 (13) Thus, (f g)(x) = f(g(x)) = 3x2 3 x 4 Let's try one more composition but this time with 3 functions It'll be exactly the same but with one extra step Find (f g h)(x) given f, g, and h{1}\right\rbrace} The domain of a function is all the values that \displaystyle {x} can take Shura May 12, 15 The answer is D = R−{−3Compose Functions If we have two functions g(x) g ( x) and f(x) f ( x) in which we contain one within the other, we say that these are compound functions For the same reason, if f f

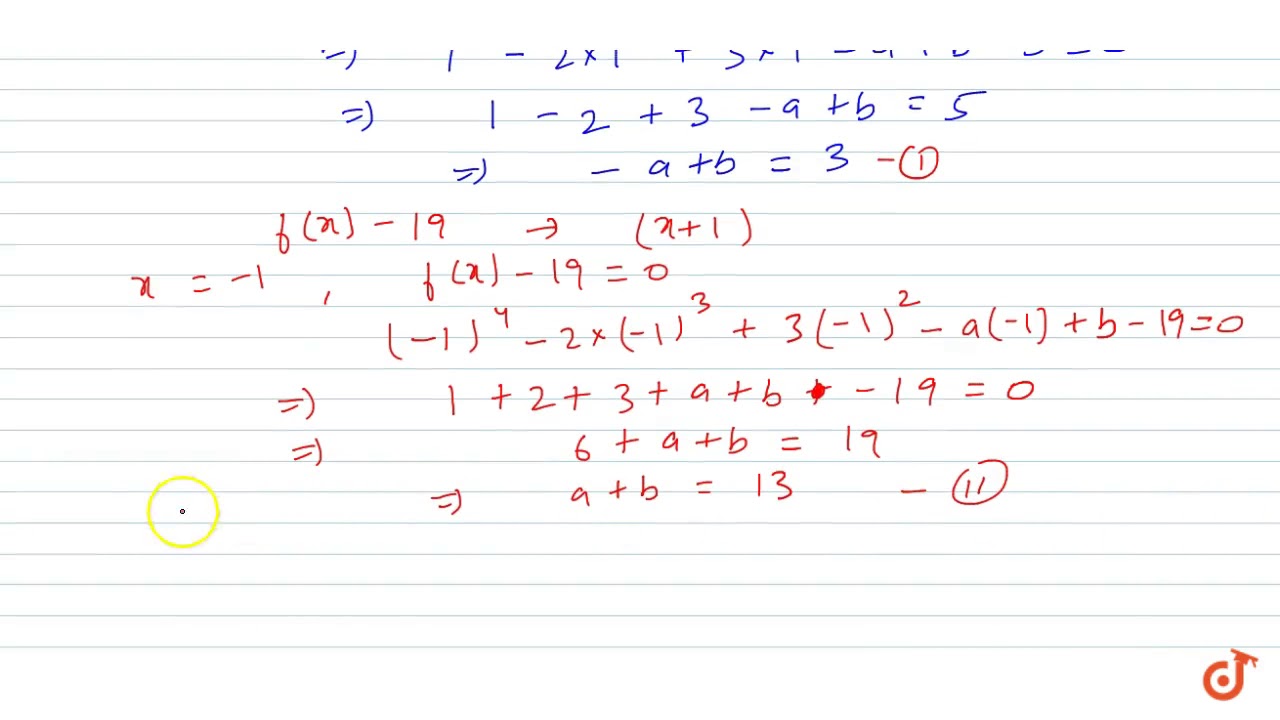
The Polynomials F X X 4 2x 3 3x 2 Ax B When Divided By X 1 And X 1 Leaves The Youtube

Apex 3 Steelseries

The Algebra of Functions Like terms, functions may be combined by addition, subtraction, multiplication or division Example 1 Given f ( x ) = 2x 1 and g ( x ) = x2 2x – 1 find ( f g ) ( x ) and ( f g ) ( 2 )F (g(x)) f ( g ( x)) Evaluate f (g(x)) f ( g ( x)) by substituting in the value of g g into f f f (x2) = 3(x2)−4 f ( x 2) = 3 ( x 2) 4 Simplify each term Tap for more steps Apply the distributive property f ( x 2) = 3 x 3 ⋅ 2 − 4 f ( x 2) = 3 x 3 ⋅ 2 4 Multiply 3 3 by 2 2 f ( x 2) = 3 x 6 − 4 f ( x 2 · 26 A property of logarithms is that logax = logbx logba, for all bases a, b>0, ≠ 1 (a) Rewrite this identity when b = e, ie, using logex = lnx (b) Use part (a) to find the derivative of y = logax (c) Give the derivative of y = log10x In Exercises 2732, compute the first four derivatives of the given function

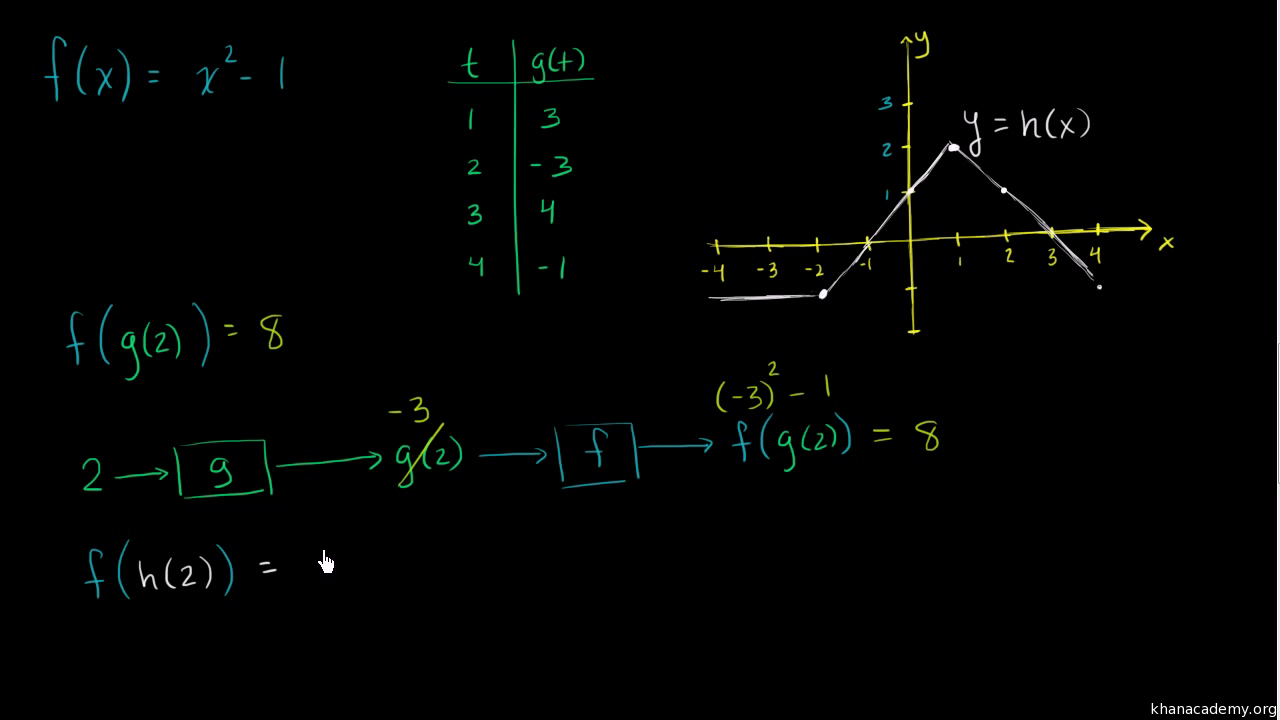
Intro To Composing Functions Video Khan Academy

Three Dimensional Space Wikipedia

By signing up, you'll get thousands of stepbystep solutions to your homework questions Let f(x) = x^2 3 x 8 and g(x) = xF(x)=x^4x^29 g(x)=x^33x^212 Doris uses 8square pieces of fabric to make one scarf Each side of a square piece of fabric is 1/4 foot in lengthG ( x) = ( x − 3) 2 1 − 2 To add or subtract expressions, expand them to make their denominators the same Multiply 2 times \frac {\left (x3\right)^ {2}} {\left (x3\right)^ {2}} To add or subtract expressions, expand them to make their denominators the same

Please Help Suppose That F X X 2 And G X 3x 2 8 Which Statement Best Compares The Graph Of G X Brainly Com

F X X 2 What Is G X Brainly Com

G (F (x))=3x^21 Click card to see definition 👆 Tap card to see definition 👆 F (x)=x^2 and G (x)=3x1 Click again to see term 👆 Tap again to see term 👆 Nice work!Find f'(a) f(x) = 3x^2 4x 1 🚨 Hurry, space in our FREE summer bootcamps is running out 🚨 · It is easy to prove that F(x)^2G(x)=c from the first line, because the first line is the derivative of that, which is zero To prove the first line, just sub in the formulas from the question and compute $\endgroup$ – Teddy Baker Sep 22 '17 at 1427

F X X 1 X 2 X 3 X 0 4 Find C If Lmvt Can Be Applied

Shifting Parabolas Video Khan Academy

Solution for f(x)=3/x7 and g(x)=x25x what is (fg)(x) Want to see this answer and more?F (x)=x^2 WolframAlpha= 2x 3 x 2 2 The domain of (f g)(x) consists of all xvalues that are in the domain of both f and g In this example, f and g both have domain consisting of all real numbers, therefore (f g)(x) also has domain consisting of all real numbers The Difference of Two Functions

Help

Shifting Functions Introduction Video Khan Academy

Answer to if f(x)=3x5 and g(x)=x5, what is f(g(x))?La funzione composta `e g(f(x)) = loge(−x3) L'insieme di definizione `e −x 3 >0 da cui segue x · f(g(x))=color(green)(3x^23x The problem with this type of question is often the confusion that results from two different uses of x If instead we write color(white)("XXX")f(color(blue)(w))=color(blue)(w)^2color(blue)(w) then there is less difficulty in replacing color(blue)(w) with color(red)(g(x)) color(white)("XXX")f(color(red)(g(x)))=color(red)(g(x))^2color(red)(g(x)) and then replacing color(red)(g(x)) with color(brown)(3x1) color(white)("XXX")f(g(x

Root Tlatex Class Reference

Centroid Wikipedia

Quarterfreelp and 30 more users found this answer helpful heart outlinedTap again to see term 👆 Which of the following will form the composite function of G (F (x)) shown below?Example 4 We wish to translate the graph of the function f(x) = x 3 – x by the vector The following table of values is for x taking values between –2 and 2 First we calculate f(x) Next we move all the outcomes down by 1 ( eg the value for x = – 2 becomes the value for x = –1)

Let G X 1 X X And F X 1 X0 Then For All X F G X Is Equal To Where Represents The Greatest Integer Function

M2 6 5 2 Apex Checkup Youtube

 · Let f(x) = x^3 x^2 3x 1 and h(x) = f(x)/g(x) where h is a rational function such that (a) it is continuous every asked Jan 21, in Limit,F (x)=2x3,\g (x)=x^25,\ (f\\circ \g) (x) f (x)=2x3,\g (x)=x^25,\ (f\ (g (x))) f (x)=2x3,\g (x)=x^25,\ (f\g) (x) f (x)=2x3,\g (x)=x^25,\f\\g precalculusfunctionarithmeticcompositioncalculator f (x)=2x3, g (x)=x^25, (f g) (x

Apex 3 Steelseries

Apex 3 Steelseries

If G Is The Inverse Of A Function F And F X 1 1 X 5 The

Identifying Horizontal Squash From Graph Video Khan Academy

Domain Of The Function F X Sqrt 2 2x X 2 Is Youtube

Home Apex Office Print

Home Apex Office Print

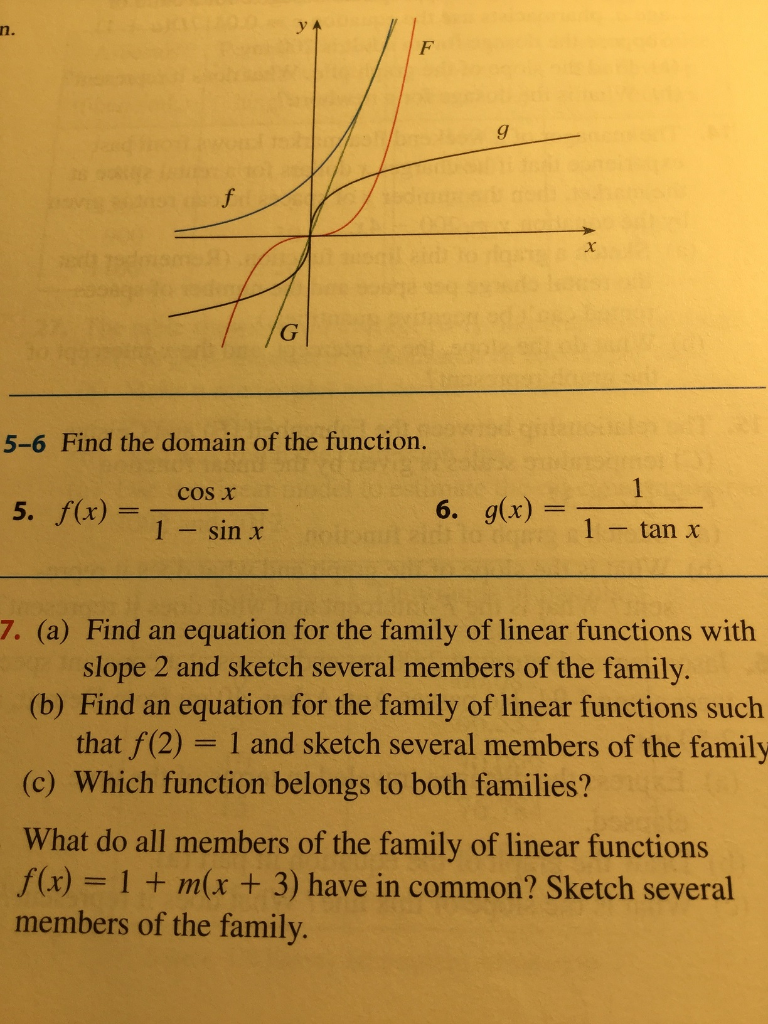
What Is The Domain Of F X Cos X Quizlet

Home Apex Office Print

What Is G X Brainly

Misc 1 F X X2 0 X 3 3x G X X2 0 X 2 3x

Multiplying Functions Video Functions Khan Academy

Example 16 Let F X X2 And G X 2x 1 Find F G Fg F G

F X X 2 What Is G X Brainly Com

How To Solve Our Three John Conway Inspired Puzzles Quanta Magazine

If F R To R And G R To R Are Defined By F X 2x 3 And G X X

Pdf L Hopital S Rule Without Derivatives

If F X 3 X 2 G X 2 X 1 F G X Brainly Com

Continental Fahrrad Der Baron Projekt 2 4

Apex Parametric Equations

Home Apex Office Print

Home Apex Office Print

Steelseries Apex Pro Mechanische Gaming Tastatur Amazon De Computer Zubehor

Identifying Function Transformations Video Khan Academy

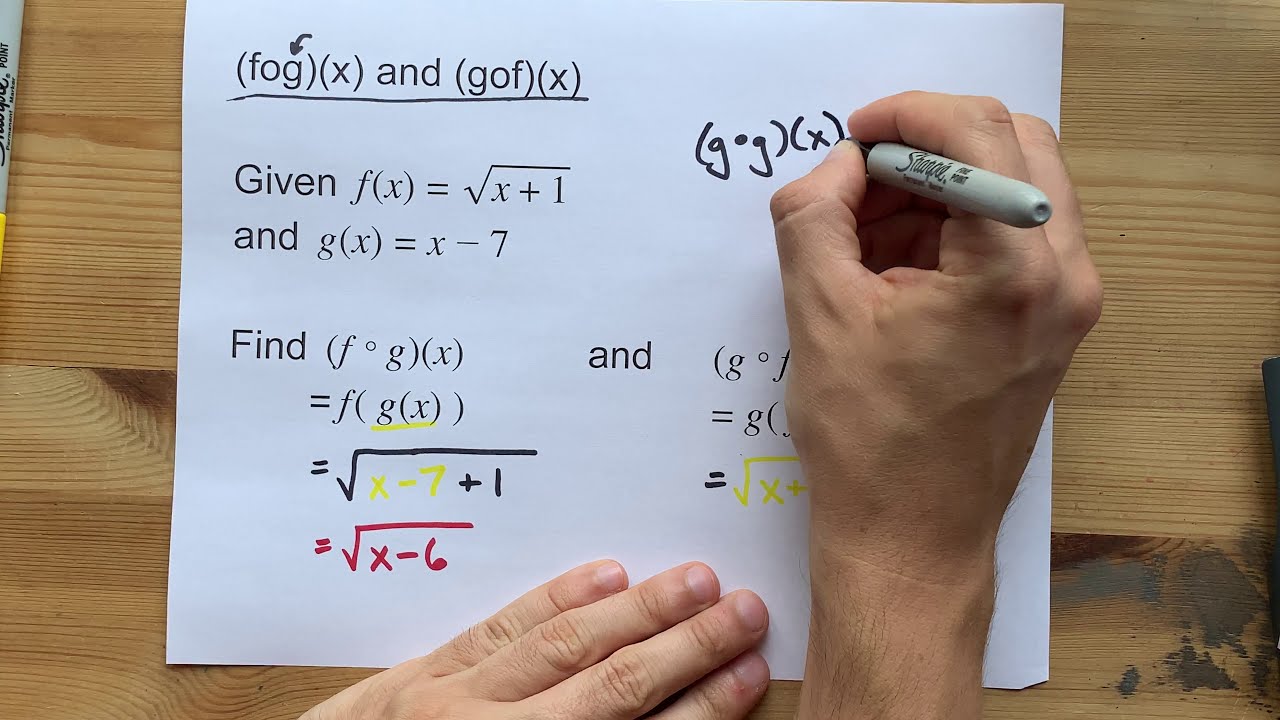
Fog X And Gof X How To Find Them Given F X And G X Youtube

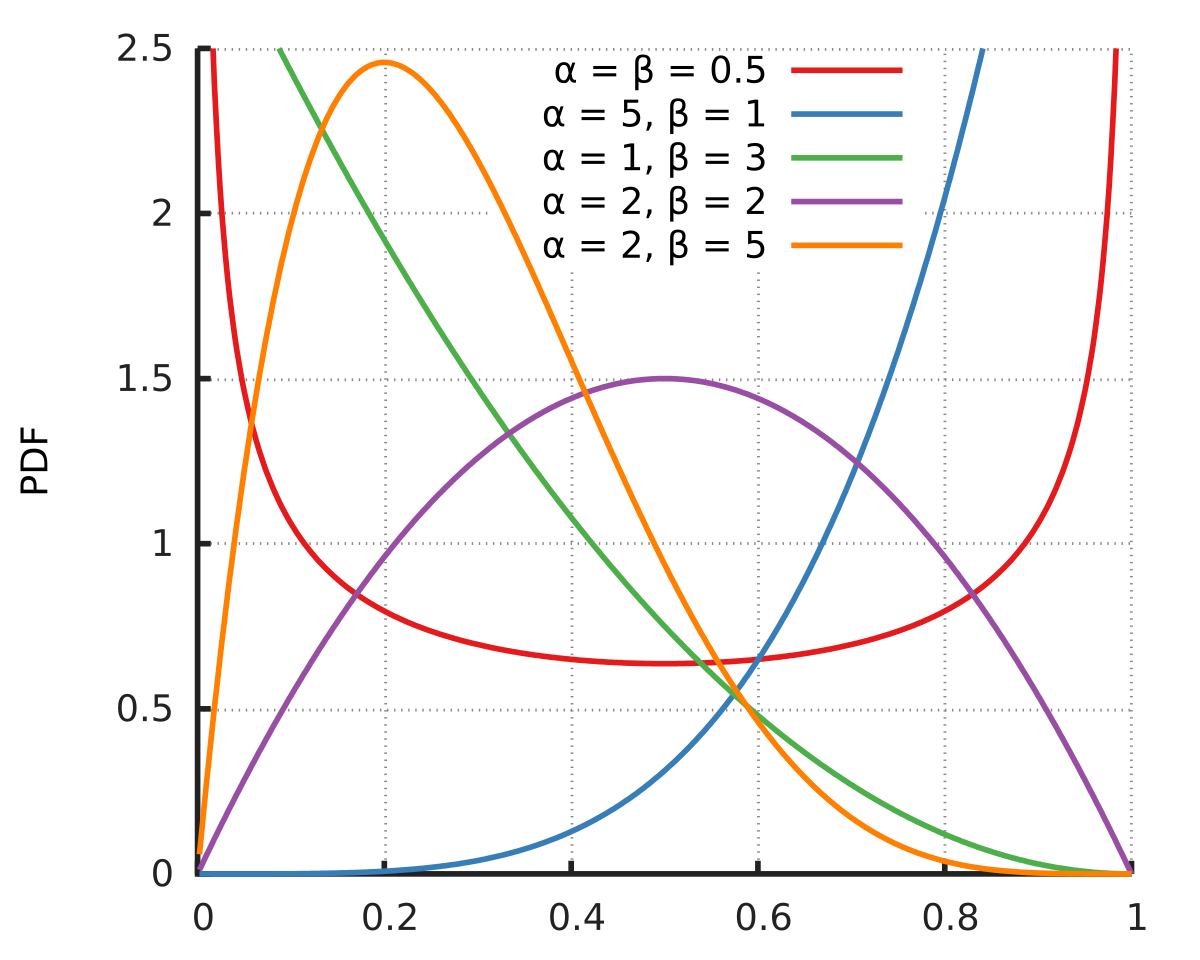
Beta Distribution Wikipedia

Example 16 Let F X X2 And G X 2x 1 Find F G Fg F G

If F X 2x And G X X 2 2 1 Then Which Of The Following Can B

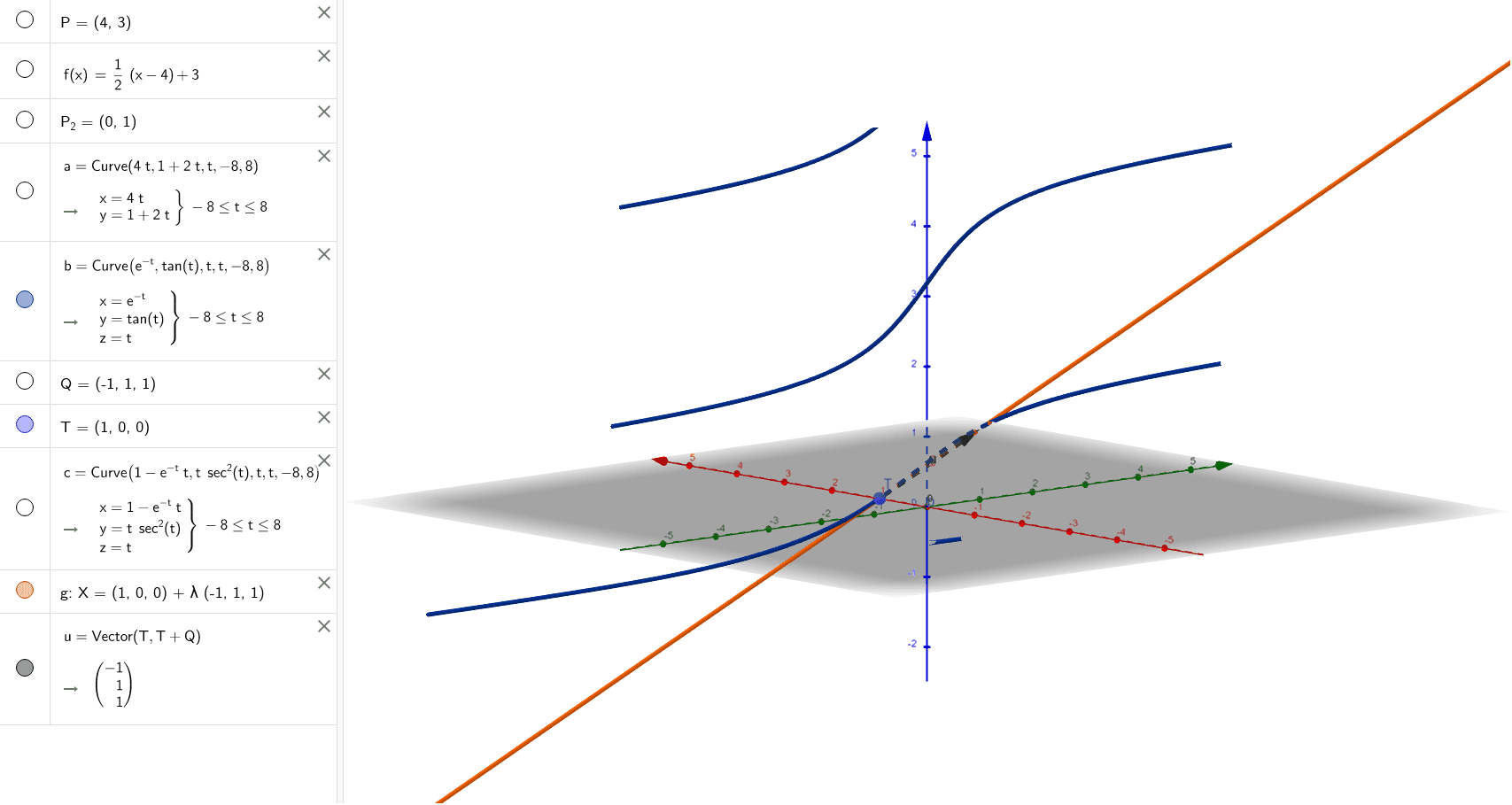
Exam 3 Apex Ch 11 Geogebra

If F X And G X Are Two Functions With G X X 1 X And F G X

Apex 3 Steelseries

Misc 1 F X X2 0 X 3 3x G X X2 0 X 2 3x

Teknor Apex Zero G Pro 3 4 In X 75 Ft Contractor Duty Kink Free Woven Green Coiled Hose In The Garden Hoses Department At Lowes Com

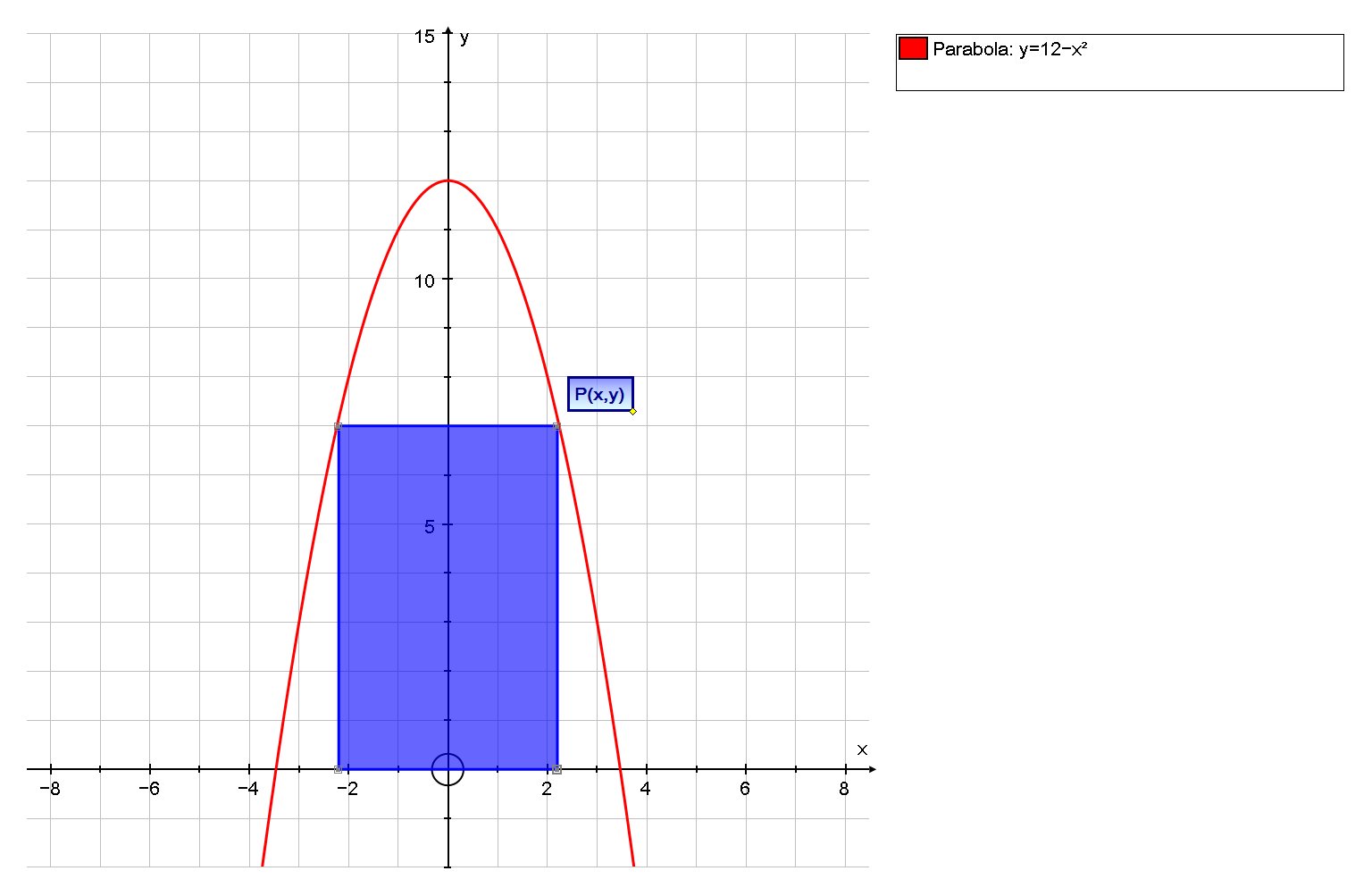
A Rectangle Is Inscribed With Its Base On The X Axis And Its Upper Corners On The Parabola Y 12 X 2 What Are The Dimensions Of Such A Rectangle With

What Is G X Brainly

Apex Structures Enhance Water Drainage On Leaves Pnas

End Behavior Of Polynomial Functions College Algebra

F X X 2 What Is G X 1 4 Brainly

Apex Basic Differentiation Rules

Quadratic Function Wikipedia

Rna Protein Interaction Mapping Via Ms2 Or Cas13 Based Apex Targeting Pnas

If F X X 4 2x 3 3x 2 Ax B Is A Polynomial Such That When It Is Divided By X 1 And X 1 Then Remainders Are

F N R Such That F X 2x 1 2 And G Q R Such That G X

Cubic Function Wikipedia

Live Cell Mapping Of Organelle Associated Rnas Via Proximity Biotinylation Combined With Protein Rna Crosslinking Biorxiv

Apex Structures Enhance Water Drainage On Leaves Pnas

Dematiaceous Hyphomycetes From South Africa Ii Some Phialidic Species Including Chalara Transkeiensis And Zanclospora Brevispora Var Transvaalensis Two New Taxa Topic Of Research Paper In Biological Sciences Download Scholarly Article Pdf

Home Apex Office Print

If F X And G X Are Two Functions With G X X 1 X And Fog

Home Apex Office Print

Rna Protein Interaction Mapping Via Ms2 Or Cas13 Based Apex Targeting Pnas

Steelseries Apex Pro Mechanische Gaming Tastatur Amazon De Computer Zubehor

Apex Structures Enhance Water Drainage On Leaves Pnas

Inflection Point Wikipedia

Steelseries Apex Pro Mechanische Gaming Tastatur Amazon De Computer Zubehor

If F X 3x 2 And G X X 2 Then Fog X

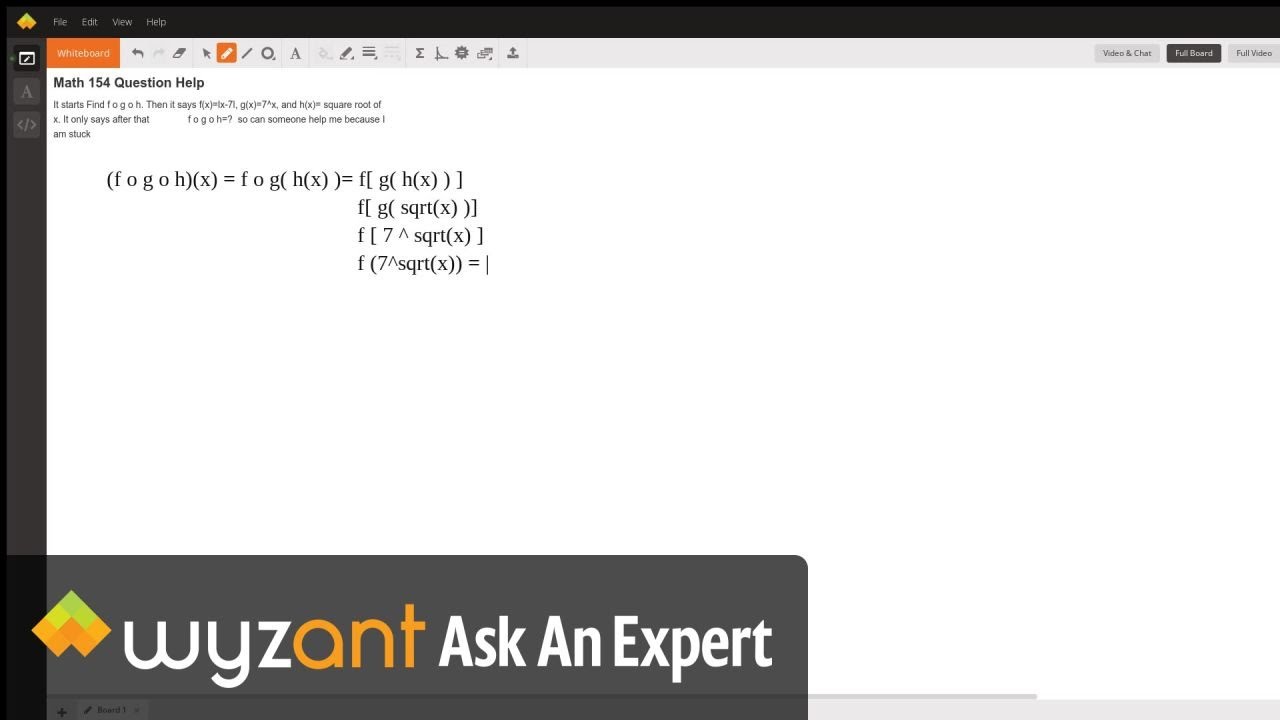
F O G O H Given F X G X And H X Youtube

Misc 3 F X X2 3x 2 Find F F X Chapter 1 Miscellaneous

Divide The Polynomial P X X 4 3x 2 4x 5 By The Polynomial G X X 2 X 1 And Find Quotient Youtube

Graphs Of Rational Functions Vertical Asymptotes Video Khan Academy